해싱이란? (Hashing)
해싱이란 임의의 길이의 값을 해시함수(Hash Function)를 사용하여 고정된 크기의 값으로 변환하는 작업을 말한다.

위 그림에서 dog 라는 문자열을 해시함수를 이용해 새로운 값으로 변환한 것을 볼 수 있는데 이 경우엔 암호화에 쓰이는 해시 알고리즘인 MD5를 사용한 것이다. 하지만 여기서 다룰 것은 암호화에 쓰인 방식이 아닌 자료구조로 사용하고자 하는 해시 테이블을 다루기 때문에 정수값으로 변환되는 해시 알고리즘을 사용한다. 해싱을 사용하여 데이터를 저장하는 자료구조를 해시 테이블(Hash Table)이라고 하며 이는 기존 자료구조인 이진탐색트리나 배열에 비해서 굉장히 빠른 속도로 탐색, 삽입, 삭제를 할 수 있기 때문에 컴퓨터 공학도라면 반드시 알아야 한다.
해시 테이블
해시 테이블이란 해시함수를 사용하여 변환한 값을 색인(index)으로 삼아 키(key)와 데이터(value)를 저장하는 자료구조를 말한다. 기본연산으로는 탐색(Search), 삽입(Insert), 삭제(Delete)가 있다.
1. Direct Address Table
먼저 가장 간단한 형태의 해시테이블로 이름 뜻대로 키 값을 주소로 사용하는 테이블을 말한다. 이는 키 값이 100이라고 했을 때 배열의 인덱스 100에 원하는 데이터를 저장하는 것이다.

위 그림에선 키 값이 21였기 때문에 인덱스 21에 원하는 데이터를 저장한 경우이다. 이러한 자료구조는 탐색,삽입,삭제 연산을 모두 $O(1)$ 에 할 수 있지만 다음과 같은 한계점이 있다.
- 최대 키 값에 대해 알고 있어야 한다.
- 최대 키 값이 작을 때 실용적으로 사용할 수 있다.
- 키 값들이 골고루 분포되어있지 않다면 메모리 낭비가 심할 수밖에 없다.
2. Hash Table
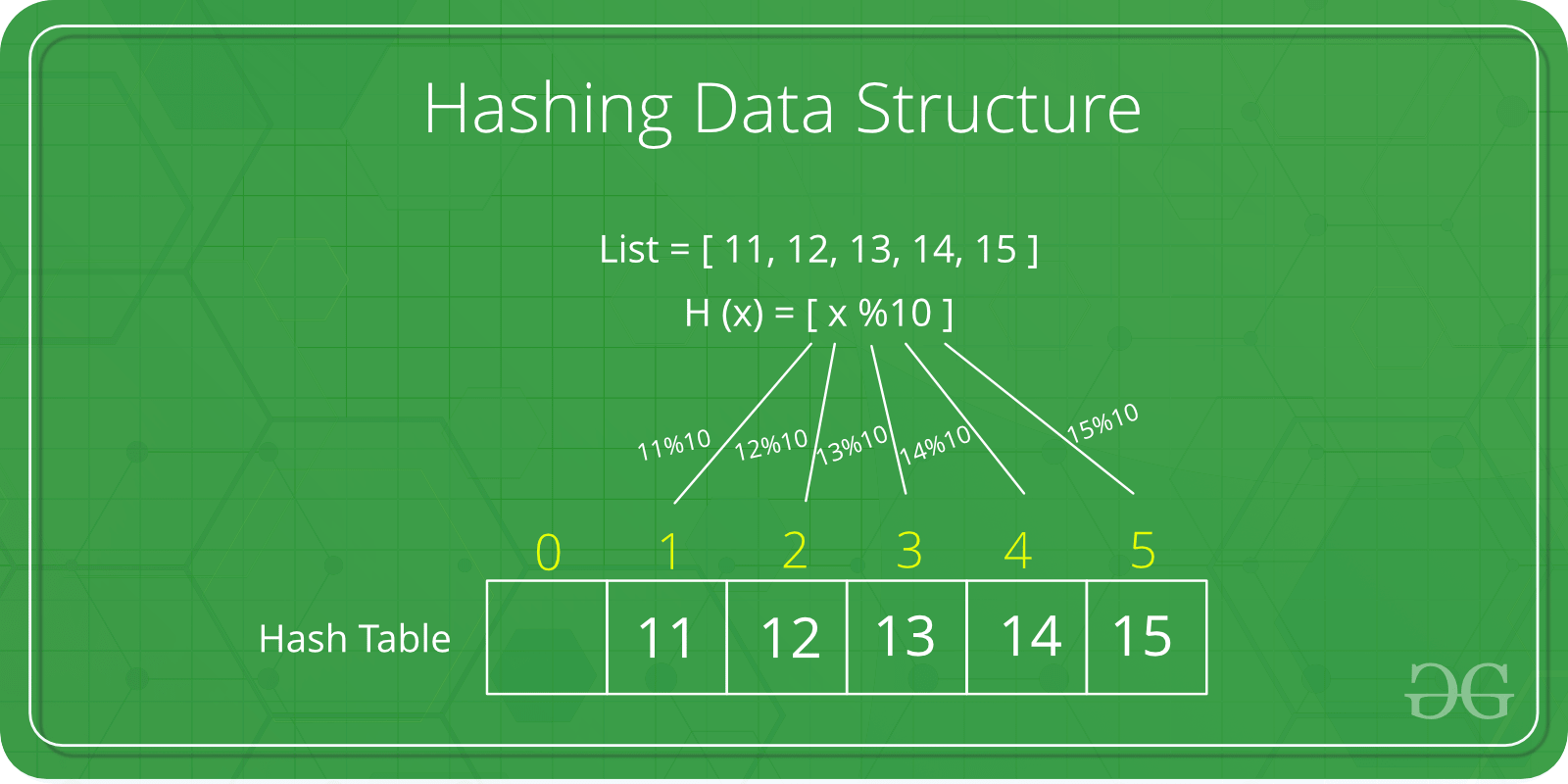
해시함수를 사용하여 특정 해시값을 알아내고 그 해시값을 인덱스로 변환하여 키 값과 데이터를 저장하는 자료구조이다. 이는 보통 알고 있는 해시 테이블을 얘기하며 개념자체가 어려운 것은 아니지만 문제가 되는 것은 충돌(Collision)이다. 충돌에 대해서 이해하기 위해선 먼저 적재율(Load Factor)에 대해서 이해해야 한다.
적재율이란 해시 테이블의 크기 대비, 키의 개수를 말한다. 즉, 키의 개수를 $K$, 해시 테이블의 크기를 $N$ 이라고 했을 때 적재율은 $K/N$ 이다. Direct Address Table은 키 값을 인덱스로 사용하는 구조이기 때문에 적재율이 1 이하이며 적재율이 1 초과인 해시 테이블의 경우는 반드시 충돌이 발생하게 된다.
만약, 충돌이 발생하지 않다고 할 경우 해시 테이블의 탐색, 삽입, 삭제 연산은 모두 $O(1)$ 에 수행되지만 충돌이 발생할 경우 탐색과 삭제 연산이 최악에 $O(K)$ 만큼 걸리게 된다. 이는 같은 인덱스에 모든 키 값과 데이터가 저장된 경우로 충돌이 전부 발생했음을 말한다. 따라서, 충돌을 최대한으로 줄여서 연산속도를 빠르게 하는 것이 해시 테이블의 핵심인데 이에 중요하게 작용하는 것이 바로 해시함수를 구현하는 해시 알고리즘이다. 해시 알고리즘이 견고하지 못하게 되면 해시함수로 도출된 값들이 같은 경우가 빈번하게 발생하게 되므로 잦은 충돌로 이어지게 되는 것이다.
결론적으로 해시 테이블의 중점사항은 충돌을 완화하는 것이며 방법으로는 2가지가 있다.
- 해시 테이블의 구조 개선
- 해시 함수 개선
이제 차근차근 알아보도록 하자.
충돌해결 1 : 해시 테이블의 구조 개선
Chaining

체이닝이란 충돌이 발생했을 때 이를 동일한 버킷(Bucket)에 저장하는데 이를 연결리스트 형태로 저장하는 방법을 말한다. 위 그림을 보면 John Smith 와 Sandra Dee 의 인덱스가 152 로 충돌하게 된 경우인데, 이 때 Sandra Dee 를 John Smith 뒤에 연결함으로써 충돌을 처리하는 것을 볼 수 있다.
체이닝을 통해 해시테이블을 구현했을 때의 시간복잡도는 어떻게 될까? 삽입의 경우 연결리스트에 추가하기만 하면 되기 때문에 상수시간인 $O(1)$ 이 걸리지만 탐색과 삭제의 경우는 최악일 때 키 값의 개수인 $K$ 에 대해 $O(K)$ 가 걸리게 된다. 하지만 최악의 경우 보다는 시간복잡도를 적재율을 이용해서 평균으로 표현하는 것이 일반적이다.
적재율 $\alpha$ 를 $K/N$ 이라고 하면 이 말의 뜻은 곧 해시 테이블 내에 공간 대비 키 값들이 얼마나 있느냐, 즉 충돌할 여지가 얼마나 있느냐의 뜻이다. 이를 시간복잡도에 적용하면 $O(\alpha+1)$ 이라고 하는데 정확한 증명은 찾을 수 없었다. 어쨌든 말의 의미를 파악했으니 이렇게 알아두자.
Open Addressing
원래라면 해시함수로 얻은 해시값에 따라서 데이터와 키값을 저장하지만 동일한 주소에 다른 데이터가 있을 경우 다른 주소도 이용할 수 있게 하는 기법이다.
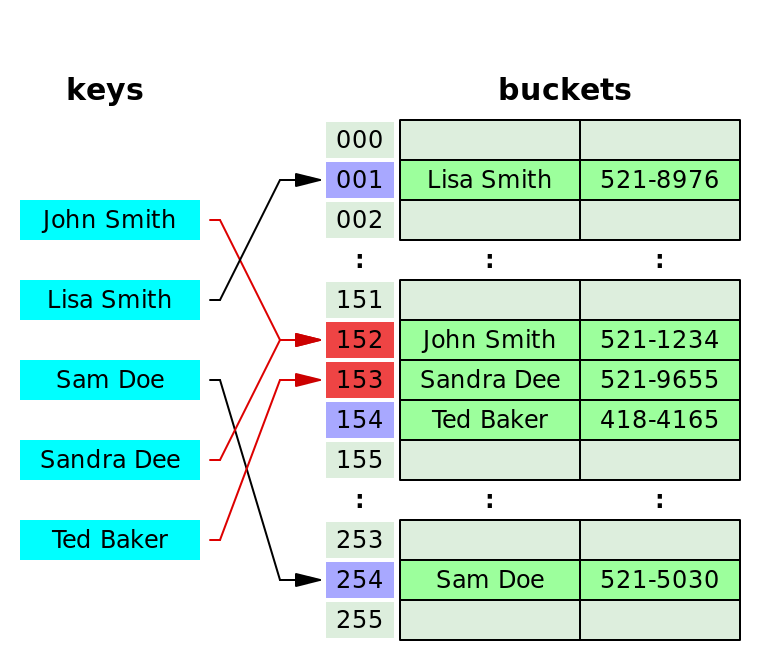
위에서 살펴본 동일한 충돌에 대해서 이번엔 체이닝 방식을 적용하지 않고 그 다음으로 비어있는 주소인 153 에 저장하는 것을 볼 수 있다. 이러한 원리로 탐색, 삽입, 삭제가 이루어지는데 다음과 같이 동작한다.
- 삽입: 계산한 해시 값에 대한 인덱스가 이미 차있는 경우 다음 인덱스로 이동하면서 비어있는 곳에 저장한다. 이렇게 비어있는 자리를 탐색하는 것을 탐사(Probing)라고 한다.
- 탐색: 계산한 해시 값에 대한 인덱스부터 검사하며 탐사를 해나가는데 이 때 “삭제” 표시가 있는 부분은 지나간다.
- 삭제: 탐색을 통해 해당 값을 찾고 삭제한 뒤 “삭제” 표시를 한다.
이러한 open addressing 방식은 3가지 방법을 통해서 해시 충돌을 처리한다.
Open Addressing의 3가지 충돌 처리기법
선형탐사(Linear Probing)

선형탐사는 가장 기본적인 충돌해결기법으로 위에서 설명한 기본적인 동작방식이다. 선형탐사는 바로 인접한 인덱스에 데이터를 삽입해가기 때문에 데이터가 밀집되는 클러스터링(Clustering) 문제가 발생하고 이로인해 탐색과 삭제가 느려지게 된다.
제곱탐사(Quadratic Probing)
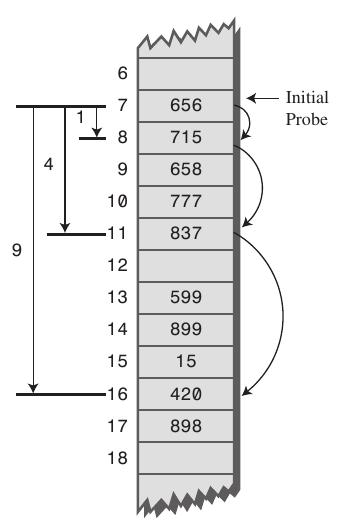
제곱탐사는 말 그대로 $1^2, 2^2, 3^2..$ 으로 탐사를 하는 방식으로 선형탐사에 비해 더 폭넓게 탐사하기 때문에 탐색과 삭제에 효율적일 수 있다. 하지만 이는 초기 해시값이 같을 경우에 탐사하는 역시나 클러스터링 문제가 발생하게 된다.
이중해싱(Double Hashing)
이중해싱은 선형탐사와 제곱탐사에서 발생하는 클러스터링 문제를 모두 피하기 위해 도입된 것이다. 처음 해시함수로는 해시값을 찾기 위해 사용하고 두번째 해시함수는 충돌이 발생했을 때 탐사폭을 계산하기 위해 사용되는 방식이다.
비교
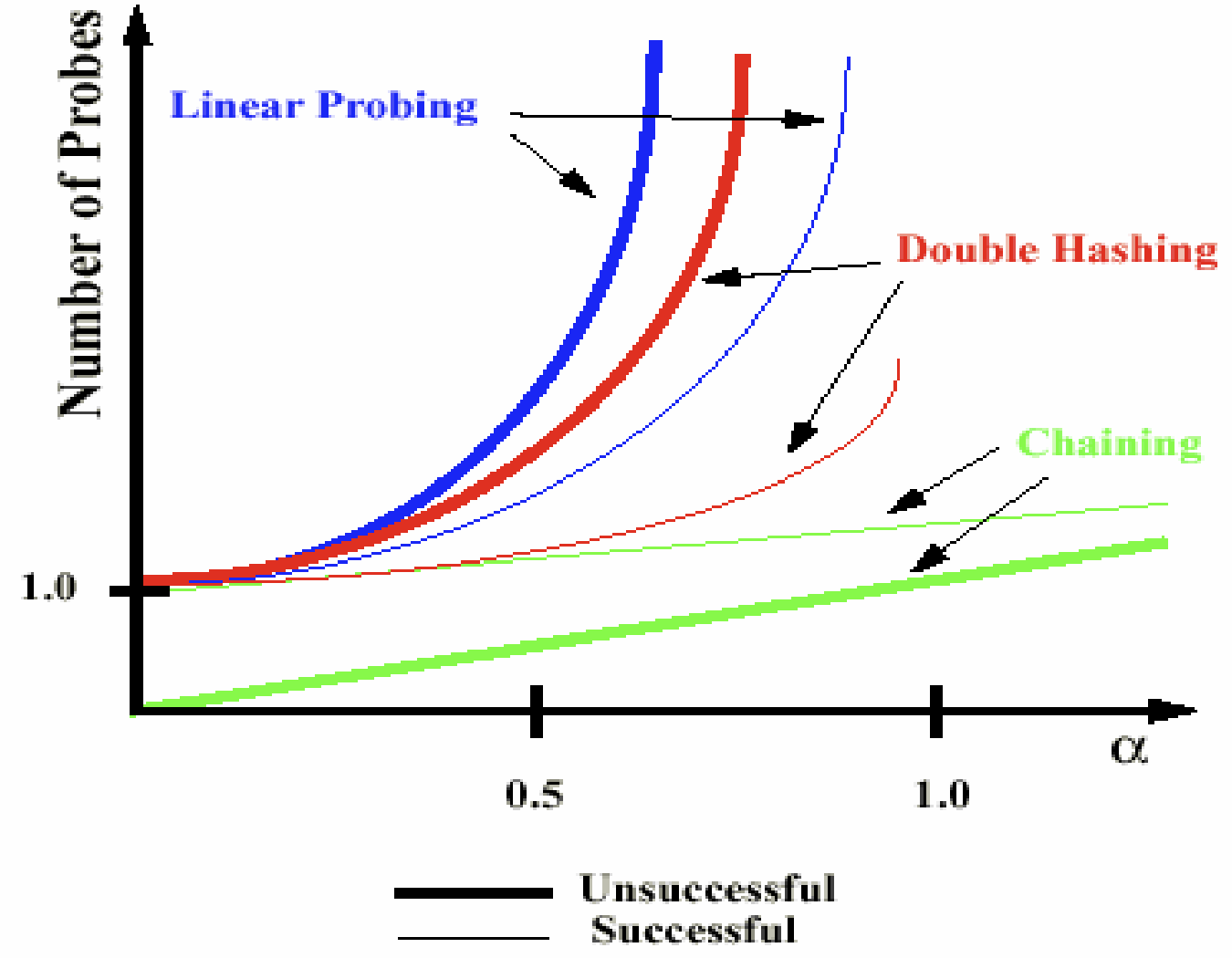
위에서 배운 충돌해결기법들을 비교해보면 적재율인 $\alpha$ 에 따라서 위와 같이 나오는데, 여기서 successful search는 찾고자 하는 데이터가 해시테이블에 있는 경우이고 unsuccessful search는 없는 경우이다.
충돌해결 2 : 해시 함수 개선
나눗셈법(Division Method)
아주 간단하게 해시값을 구하는 방법으로 미리 해시 테이블의 크기인 $N$ 을 아는 경우에 사용할 수 있다. 해시함수를 적용하고자 하는 값을 $N$ 으로 나눈 나머지를 해시값으로 사용하는 방법이다. 즉 다음과 같다. $$ h(k)=k\ mod\ N $$ 여기서 $N$ 은 2의 제곱꼴을 사용하면 안된다고 하는데 이는 그 제곱꼴이 $2^p$ 로 나타날 때 $k$ 의 하위 $p$ 개의 비트를 고려하지 않는다고 한다. 따라서 $N$ 은 소수(Prime Number)를 사용하는 것이 좋다.
곱셈법(Multiplication Method)
$0<A<1$ 인 $A$ 에 대해서 다음과 같이 구할 수 있다. $$ h(k)=\lfloor N(kA\ mod\ 1)\rfloor $$ $kA\ mod\ 1$ 의 의미는 $kA$ 의 소수점 이하 부분을 말하며 이를 $N$ 에 곱하므로 0부터 $N$ 사이의 값이 된다. 이 방법의 장점은 $N$ 이 어떤 값이더라도 잘 동작한다는 것이며 $A$ 를 잘 잡는 것이 중요하다.
이외에도 다양한 해시 함수가 있다는 것만 알아두도록 하자.
구현
구조는 체이닝을 사용했고 해시 함수로는 아스키코드를 더하는 방식을 이용했다.
#include <iostream>
#include <string>
using namespace std;
class Node {
private:
string key;
int value;
Node* nextNode;
public:
Node() : key(""),value(0),nextNode(NULL) {}
Node(string _key, int _value){
key = _key;
value = _value;
nextNode = NULL;
}
Node* getNext() { return nextNode; }
void setNext(Node* next) { nextNode = next; }
string getKey() { return key; }
int getValue() { return value; }
};
class HashTable {
private:
int size;
Node* nodeList;
int hashFunction(string s) {
int len = s.length();
int hash = 0;
for(int i=0; i<len; i++){
hash += s[i];
}
return hash%size;
}
public:
HashTable(int _size) {
size = _size;
nodeList = new Node[_size];
}
void put(string key, int value) {
int index = hashFunction(key);
Node* next = nodeList[index].getNext();
Node* cur = &nodeList[index];
while(next != NULL) {
cur = next;
next = next->getNext();
}
Node* newNode = new Node(key,value);
cur->setNext(newNode);
}
Node get(string key) {
int index = hashFunction(key);
cout << "해시 값: " << index << '\n';
Node* cur = nodeList[index].getNext();
while(cur!=NULL) {
if(!key.compare(cur->getKey())) {
return *cur;
}
cur = cur->getNext();
}
return Node();
}
~HashTable() {
for(int i=0; i<size; i++){
Node* cur = nodeList[i].getNext();
while(cur!=NULL) {
Node* temp = cur->getNext();
delete cur;
cur = temp;
}
}
delete[] nodeList;
}
};
int main(void)
{
HashTable hashTable = HashTable(100);
hashTable.put("ac",10);
hashTable.put("bb",12);
cout << hashTable.get("ac").getValue() << '\n';
cout << hashTable.get("bb").getValue() << '\n';
return 0;
}
ac 와 bb 는 196으로 아스키 코드값의 합이 같기 때문에 테이블 크기로 나눈 값은 96으로 같다. 그러나 체이닝을 이용했기 때문에 충돌이 발생함에도 불구하고 찾을 수 있다는 것을 확인할 수 있다.