개념
기존 세그먼트 트리에서 하나의 리프노드를 업데이트 할 때 $O(lgN)$ 이 걸리기 때문에 구간 업데이트에 관련된 문제가 나올 경우 최대 $O(NlgN)$ 이 걸려서 시간초과를 받게 된다. 따라서 이를 위해 다른 알고리즘이 필요한데 바로 이러한 구간 업데이트를 단 $O(lgN)$ 만에 수행할 수 있는 테크닉이 lazy propagation이다. 이름의 뜻 그대로 게으르게(lazy) 전파(propagation) 한다는 것으로 특정 업데이트 구간에 포함되는 노드들에게 나중에 전파시킬 값을 저장해 둠으로써 다음 업데이트나 쿼리를 할 때 마다 자식노드들 한테만 전파해주면 되게 된다.
위 방식을 구현하기 위해서 각 노드는 lazy 배열을 가지며 이는 다음 업데이트나 쿼리에 대해서 현재 노드를 포함한 모든 자식 노드들에 적용되는 값을 가지는 배열을 뜻한다. 이를 통해 한번에 업데이트 하지 않고 lazy 배열을 참조하며 업데이트가 필요할 때만 해줄 수 있게 된다.
배열 [1,5,6,2,4] 에 대해서 구간합 예시를 통해 어떻게 동작하는지 살펴보도록 하자.
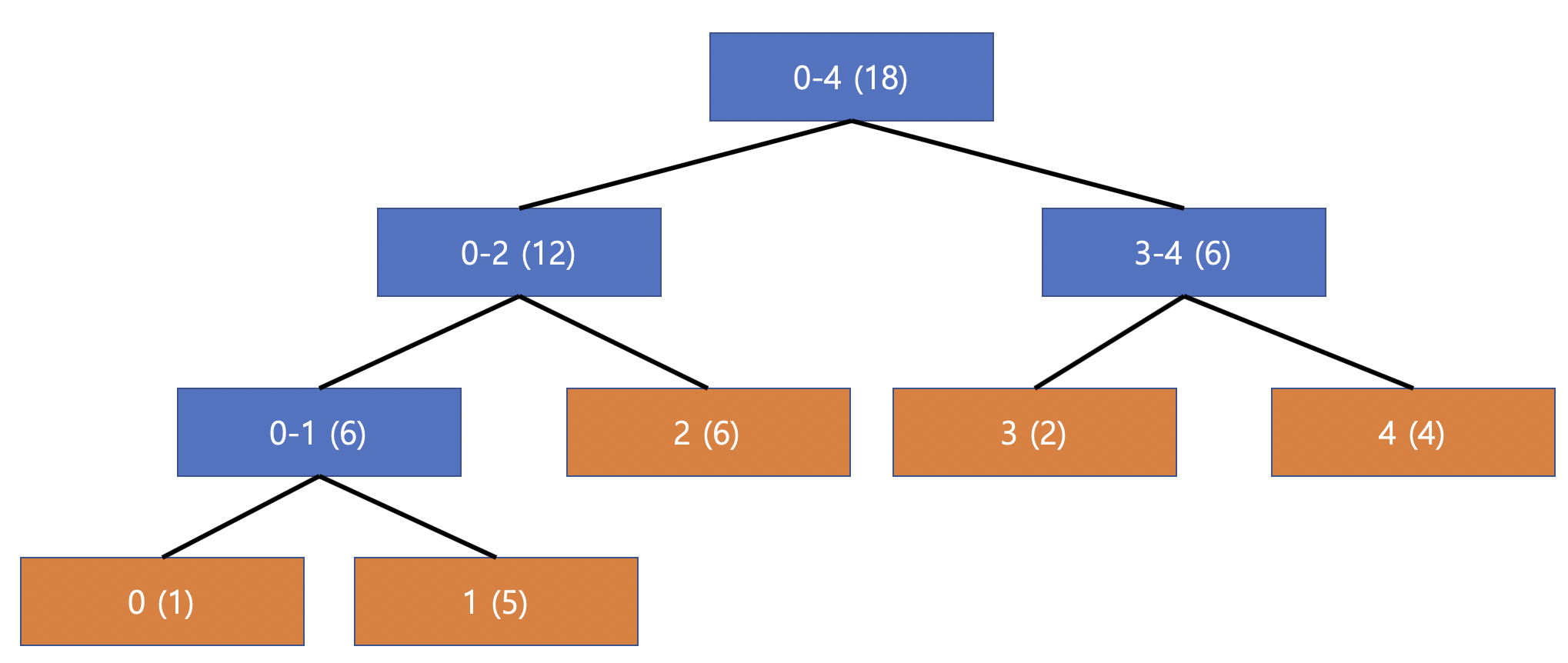
세그먼트 트리는 위와 같이 구성됨을 알 수 있고 여기서 구간 0~1 에 3을 더한다고 해보자.
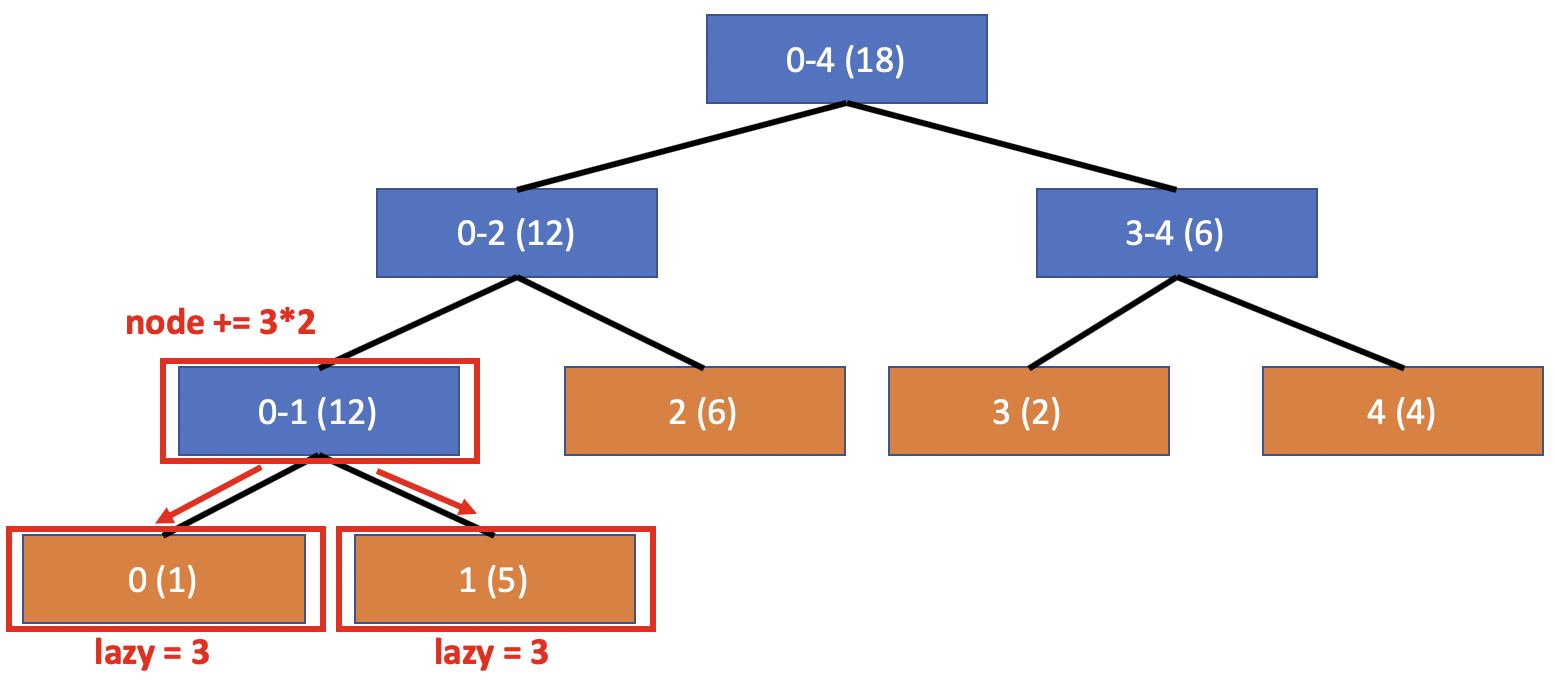
위 그림의 뜻은 0-1 에 해당하는 노드 하위 노드들에게 더할 값이 3 이 있고 현재 노드를 업데이트 해주자는 것이다. 단, 주의할 점은 현재 노드에 업데이트 해줄 때 자식노드들의 개수를 곱해줘야 한다는 것을 꼭 기억하자! 여기서 자식 노드들에게 초기화시킨 lazy 배열의 값은 나중에 다시 업데이트를 하거나 쿼리를 날릴 때 해당 값을 사용하여 자식들을 업데이트하고 propagation을 시키기 위함이다. 이를 보기 위해 이번엔 구간 쿼리인 1-2 를 날렸다고 해보자.
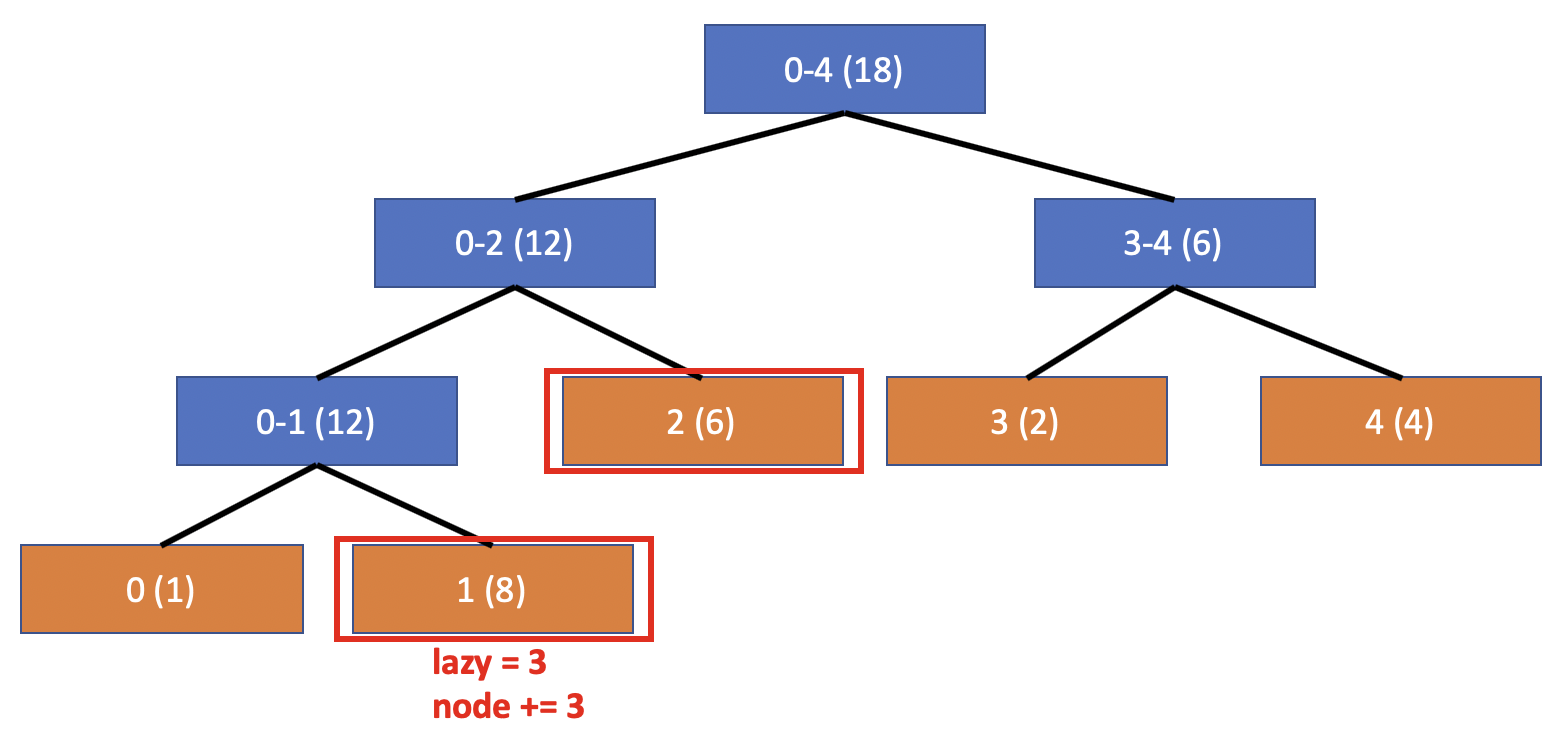
그럼 위와 같이 쿼리를 날리게 되면 먼저 lazy 값을 가지는지 확인을 한 다음 자식으로 propagation을 시키는데, 위의 경우는 리프노드가 lazy 값을 가지고 있기 때문에 바로 노드에 더해버린다. 정리해보면 다음과 같다.
- 구간 업데이트
- Propagation
- 업데이트 구간 안에 속하는 경우, 현재노드 업데이트 해주고 자식의
lazy값 업데이트 - 나머지는 기존 세그먼트 트리의 업데이트와 동일
- 구간 쿼리
- Propagation
- 나머지는 기존 세그먼트 트리의 쿼리와 동일
- Propagation
lazy값 있는지 확인- 해당
lazy값으로 현재 노드 업데이트 - 리프노드가 아닐 경우 자식으로 전파
- 마지막에 현재 노드의
lazy값을 초기화 → 업데이트 해주었으니 나중을 위해서 초기화해야함
구간합 구현
구간 합 구하기 2 를 구현한 소스코드이다.
구간 업데이트
void update(int node, int s, int e, int l, int r, ll add)
{
propagate(node,s,e);
if(r<s || l>e) return;
if(l<=s && e<=r){
segTree[node] += (e-s+1)*add;
if(s!=e){
lazy[node*2] += add;
lazy[node*2+1] += add;
}
return;
}
update(node*2,s,(s+e)/2,l,r,add);
update(node*2+1,(s+e)/2+1,e,l,r,add);
segTree[node] = segTree[node*2]+segTree[node*2+1];
}
구간 쿼리
ll query(int node, int s, int e, int l, int r)
{
propagate(node,s,e);
if(r<s || l>e) return 0;
if(l<=s && e<=r) return segTree[node];
return query(node*2,s,(s+e)/2,l,r)+query(node*2+1,(s+e)/2+1,e,l,r);
}
Propagation
void propagate(int node, int s, int e)
{
if(lazy[node]){
segTree[node] += (e-s+1)*lazy[node];
if(s!=e){
lazy[node*2] += lazy[node];
lazy[node*2+1] += lazy[node];
}
lazy[node] = 0;
}
}