다른 분야도 약하긴 하지만, 문자열이 상당히 약하기 때문에 전에 대충 공부했던 KMP를 다시 꺼내들어서 공부했다. 상당히 어려운 알고리즘이었고 이해하는데 꽤 오랜 시간이 걸렸다. 까먹으면 안되겠지만 혹시 몰라서 까먹을 나중을 위해서 공들여 정리하고자 한다.
개요
KMP 알고리즘은 어떤 문자열 $H$와 $S$가 주어졌고 $H$가 $S$보다 긴 경우에, $H$ 안에 $S$가 포함되어 있는지를 탐색하는 알고리즘이다. 자, 생각을 해보자. 예를 들어 단순 브루트 포스로 $S$를 탐색한다면 상당히 오랜 시간이 걸릴 수밖에 없다.
예를 들어, ABAABAA라는 문자열 $H$에서 부분문자열 ABAC를 찾기 위해선 아래와 같이 찾아야 한다.
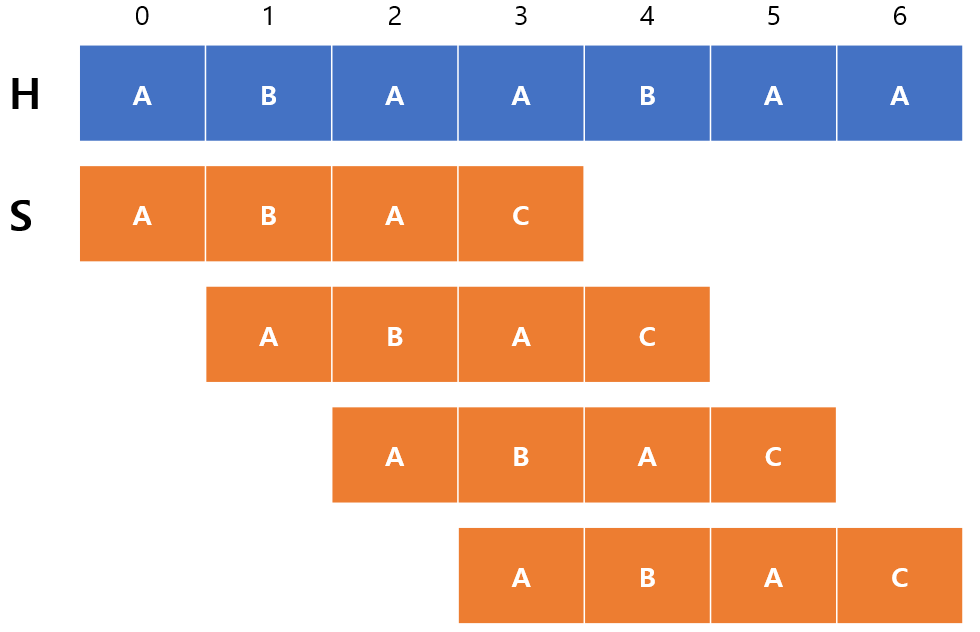
당연하게도 시간복잡도는 $H$의 길이를 n, $S$의 길이를 m이라고 했을 때 $O(nm)$이 나오게 되기 때문에 비효율적이라는 것을 한눈에 알 수 있다. 그럼 어떻게 개선할 수 있을까?
위 그림에서 처음 비교를 할 때 ABA까지는 일치하지만 C에서 불일치한다는 것을 볼 수 있다. KMP는 이 점을 착안해서 ABA까지 일치하니까 인덱스를 1만 옮기지 말고, 일치한 부분은 옮겨도 된다고 말한다. 즉, 이미 얻은 정보를 활용하여 문자열 $S$를 빠르게 옮기는 것이다.
핵심 개념
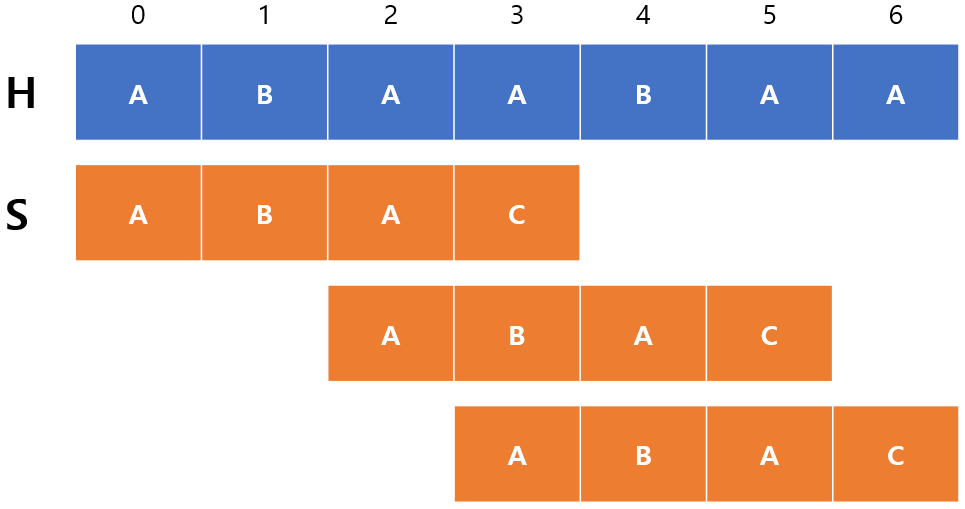
그럼 위에서 말한대로 ABA까지 일치하니까 한번에 옮기면 되는 것일까? 아래 그림을 보자.

ABA를 건너뛰고 한번에 옮겼더니 원래 계산해야 될 1번째,2번째 인덱스를 생략할 수 있었다. 그러나 빼먹은 부분이 있으니 바로 ABA는 반복되는 부분문자열이 있다는 것이다.
이 말은 ABA가 일치하긴 해도 그 안에 $S$가 시작할 수 있는 부분이 존재할 여지가 있기 때문에 반드시 ABA에서 시작할 수 있는지 없는지를 확인해주어야 한다.
그렇다면 어디에서 시작해야 할까? 접두사와 일치하는 접미사가 있는지를 확인해주면 된다. 왜냐하면 일치하는 문자열은 이미 $S$에 속한 문자열이기 때문에 또다른 $S$의 시작점을 찾는 것이 핵심이기 때문이다. 그 시작점을 찾는 것이 바로 접미사에서 접두사와 같은 부분이 있는지를 확인하는 것임을 알 수 있다.
ABA는 A가 접미사이면서 접두사가 되기 때문에 앞쪽의 AB를 건너뛸 수 있게 되므로 아래그림과 같이 2번째 인덱스부터 비교하면 되는 것이다.
결국 이 말은 $S$에서 0번째 인덱스를 제외한 다른 인덱스들에 대해 접두사와 접미사가 일치하는 부분을 알아야 한다는 것이다. 그래야 그만큼을 탐색하지 않고 건너뛸 수 있기 때문에 따로 그 값을 미리 구해놓아야 한다. (0번째 인덱스를 제외하는 이유는 문자 1개밖에 없기 때문)
이 값을 사용하는 경우는 불일치가 발생했을 때 이기 때문에, 실패했을 때 어떻게 해야하는지 알려준다는 점에서 실패 함수(failure function)라고 부르기도 한다.
★ 실패 함수
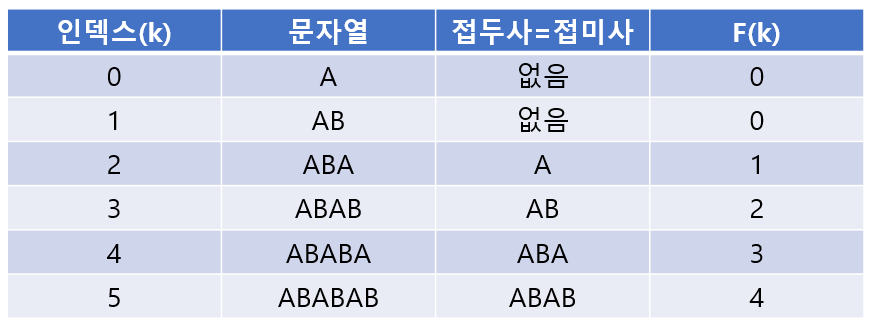
실패 함수는 KMP에서 아주 중요한 개념이고 상당히 많이 활용되기 때문에 반드시 익혀야 한다. 이번엔 예시를 좀 변경해서 $S$를 좀 더 긴 문자열로 잡고 실패 함수값을 구해보자. $S$를 ABABAB라고 하고 실패 함수를 $F(k)$라고 하면, $F(k)$의 의미는 $k$번째 인덱스에서 접두사와 접미사가 일치하는 최대길이이다. (최대인 이유는 굳이 최대로 일치하는 부분이 있음에도 불구하고 그것보다 작은 길이 만큼 건너뛰는 것은 낭비이기 때문)

위에서 말했던 것처럼 0번째 인덱스는 스킵하고 1번째 인덱스부터 보면 AB에서 접두사,접미사가 일치하는 부분이 없기 때문에 $F(1)=0$이다.
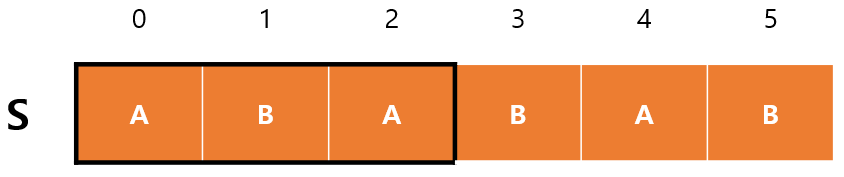
다음으로 ABA에선 A가 최대로 일치하는 부분이므로 $F(2)=1$이다.

그 다음은 ABAB이기 때문에 AB가 최대로 일치, 따라서 $F(3)=2$이다.
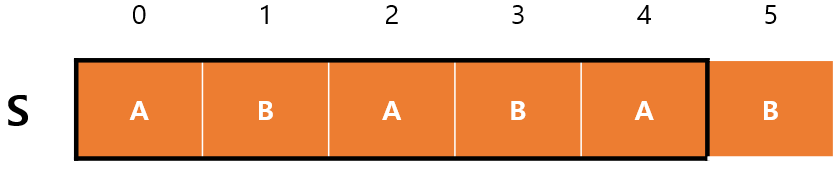
ABABA에선 ABA가 최대이므로 $F(4)=3$.
마지막으로 ABABAB에서 ABAB가 최대이므로 $F(5)=4$가 된다. (ABABAB가 아님!!)
구한 실패 함수 값들을 표로 나타내보면 다음과 같다.
그럼 실패 함수값들을 KMP에서 어떻게 활용할 수 있을까?
★ KMP 알고리즘
드디어 KMP 알고리즘이 무엇인지 좀 더 명확히 알아볼텐데 $S$는 방금 사용했던 ABABAB를 사용하고 $H$는 좀 더 긴 문자열을 사용하기로 하자. 그리고 정확한 이해를 위해 변수 $begin$을 $H$의 시작 인덱스로, 일치하는 개수를 $m$이라고 하면 아래와 같은 방식으로 동작한다.
- $H[begin+m]==S[m]$: 일치할 경우, $m$이 증가한다.
- $H[begin+m]!=S[m]$: 불일치할 경우, $begin$이 스킵하는 만큼 증가하고 $m$이 실패 함수값이 된다.
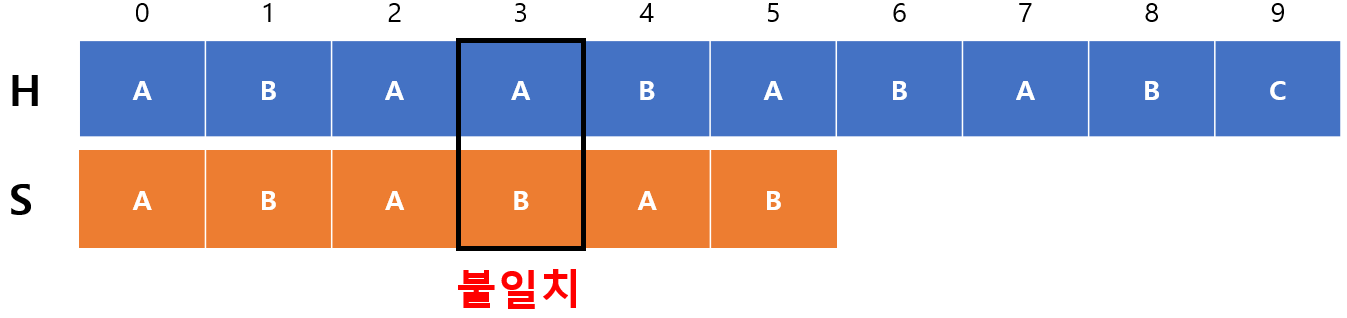
$m=3$으로 3번째 인덱스에서 불일치가 발생한 경우이다. 이 경우엔 $m-1$의 실패 함수 값을 확인하는데 $m$개가 일치했다는 것은 인덱스 $m-1$까지 일치했다는 말과 동일하기 때문이다. 위에서 구했던 것처럼 $F(2)=1$이기 때문에 다시 $S$의 1번째 인덱스부터 비교하면 된다.
왜냐하면 $F(2)=1$이란 의미가 이전에 일치한 문자열 중에 접두사와 접미사가 일치하는 부분이 1개라는 뜻이기 때문에 0번째 인덱스가 일치한다는 것이 보장되기 때문이다. 따라서, $m=1$로 초기화 되는데 이걸 일반화 하면 $m=F(m-1)$이 됨을 알 수 있다. 즉, 불일치가 발생할 경우엔 $m$값이 실패 함수값으로 초기화된다.
또한 $begin$ 값을 옮겨주어야 하는데 $begin$에 $m-F(m-1)$만큼 더해주면 된다. 이게 갑자기 왜 나왔냐 싶을지도 모르지만 생각해보면 일치하는 만큼($m$) 옮긴다음 반복되는 문자열의 길이 만큼($F(m-1)$) 빼주는 개념이다. 위 예시에선 $begin=0$인 상태에서 $m=3$을 더하면 $begin=3$이 되지만 $F(m-1)=1$을 빼주면 $begin=2$가 되기 때문에 알고리즘이 동작한다는 것을 확인할 수 있다.
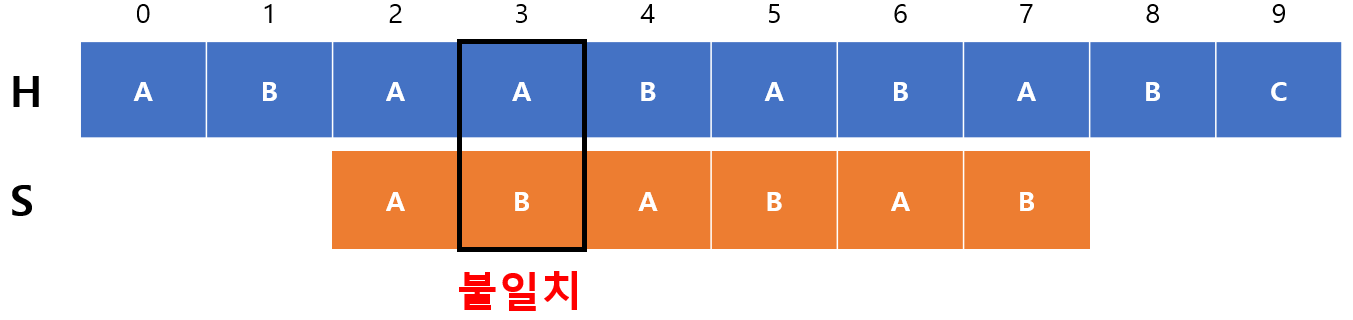
$m=1$로 옮겨진 후에 다시 비교해서 불일치가 발생하였다. $F(1-1)=F(0)=0$이기 때문에 $m=0$이되고 $begin=2+1-0=3$이 되서 다시 비교를 시작한다.
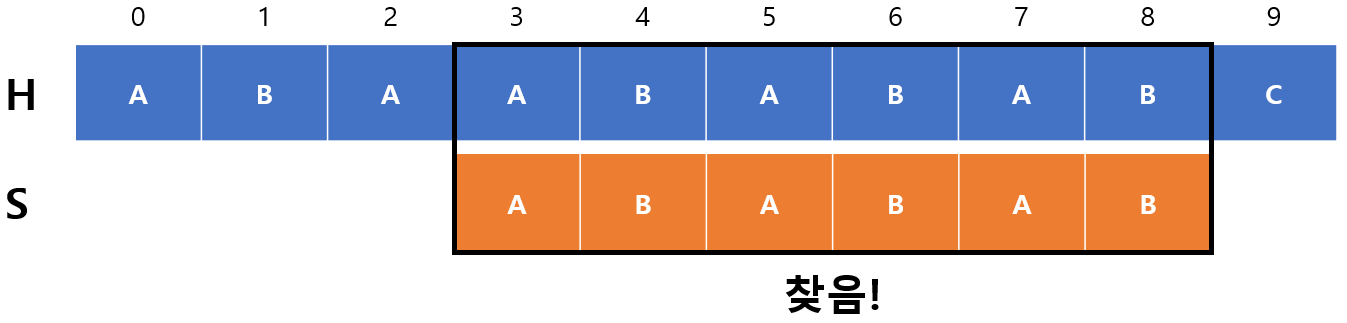
드디어 $S$를 찾았는데 이 경우에는 단순히 완전히 건너뛰면 되는 것일까? 생각해보면, 완전히 일치하는 경우에도 접두사와 접미사가 일치하는 부분이 존재한다. 즉, 현재 $m=6$인데 $F(6-1)=F(5)=4$로 4개가 일치한다는 것을 알 수 있다. $S$가 더 있을 가능성이 아직 남아있는 것이다. 따라서, $m=4$로 초기화되고 $begin=3+6-4=5$가 되는데 5부터 남은 문자개수가 5개이기 때문에 종료하게 된다. 즉, $begin$ 값이 $S$의 길이를 충족시킬 수 있을 때까지만 지속하는 것이다.
위의 모든 과정들을 이해했는가? 이해했으면 코드를 보도록 하자. (코드는 종만북을 참고!)
vector<int> kmp(const string& H, const string& S)
{
int h_len = H.length();
int s_len = S.length();
// 실패 함수값을 구해놓았다는 가정.
vector<int> f = failure_function(S);
vector<int> r(h_len-s_len+1,0);
int begin = 0, m = 0;
while(begin <= h_len-s_len) {
// 일치개수(m)가 S의 길이보다 작고
// H[begin+m]과의 문자가 일치하는 경우
if(m<s_len && H[begin+m]==S[m]){
m++;
// S를 찾은 경우에 begin값을 저장한다.
if(m == s_len) r.push_back(begin);
}
// 불일치하거나 S를 찾은 경우
else {
// 일치한적이 한번도 없고 불일치했다면 단순히 begin 옮기면 된다.
if(m==0)
begin++;
// 그게 아니라면 begin과 m을 위에서 말한 것처럼 초기화!
else {
begin += (m - f[m-1]);
m = f[m-1];
}
}
}
return r;
}
위 코드의 시간복잡도는 얼마나 될까? 최악의 경우 $H$의 모든 문자를 봐야 하기 때문에 $H$의 길이를 $H_L$이라고 한다면 $O(H_L)$이 된다. 아직 실패 함수를 계산하는 경우를 고려하진 않았지만 그래도 원래의 브루토 포스 접근보다 훨씬 빠르다는 것을 알 수 있다.
★ 실패 함수를 구하자
일단, 실패 함수의 정의를 다시 한번 되새겨보자.
0번째 인덱스를 제외한 각 인덱스에서 해당 인덱스까지의 부분문자열 중 접두사와 접미사가 일치하는 최대 길이로 $k$가 인덱스일 경우 $F(k)$로 나타낼 수 있다.
이 말을 단순하게 생각해보면 각 인덱스에서 접두사==접미사인 부분을 찾으라는 말이다. 그러나 문자열 단순 탐색이 비효율적이기 때문에 KMP에서 줄인 시간복잡도를 원상복귀 시키는 불상사가 발생할 수 있다.
그럼 어떻게 할 수 있을까? 자세히 들여다보면 KMP의 원리를 똑같이 쓸 수 있는데 그 이유를 확인해보자.
$begin$과 $m$을 똑같이 쓸텐데 헷갈릴 수 있으니 각 인덱스에서 그 값을 확인하자. 먼저 처음 값들이다.
- $begin=1$
- $m=0$
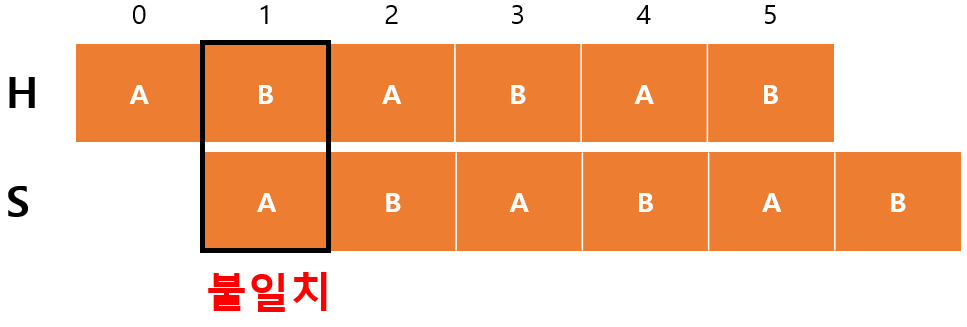
$H[begin+m]=H[1]$이 $S[m]=S[0]$과 불일치하고 $m=0$이므로 $begin$만 증가한다.
- $begin=2$
- $m=0$
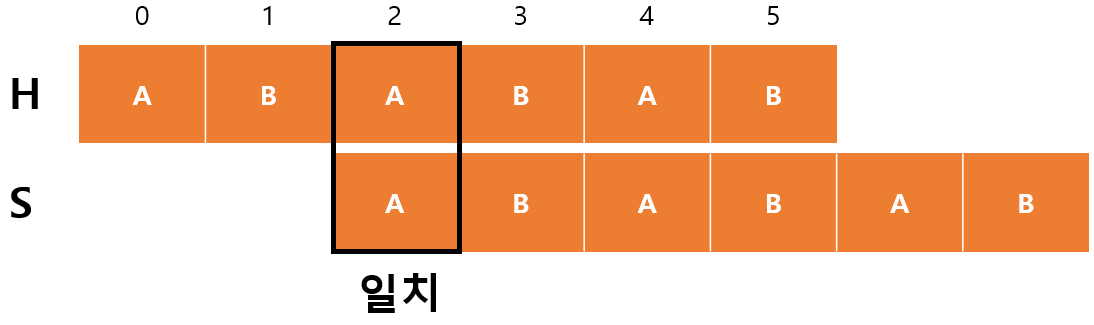
$H[2]$가 $S[0]$과 일치하기 때문에 $m$이 증가하고 $F[begin+m-1]=F[2]=1$이 된다.
- $begin=2$
- $m=1$
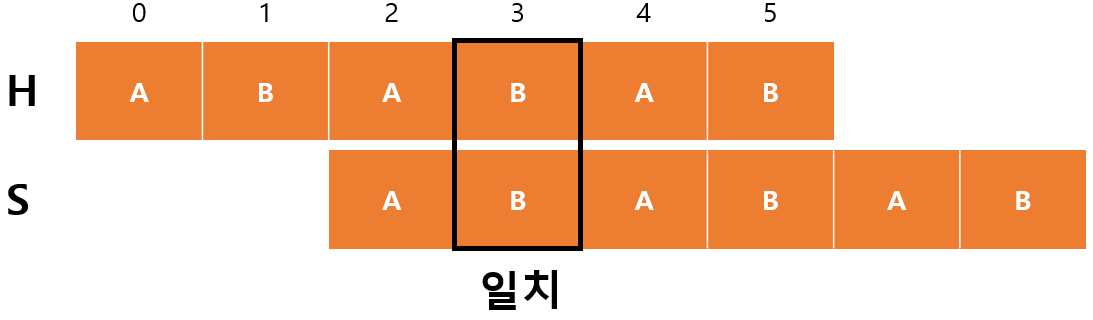
$H[3]$과 $S[1]$이 일치하기 때문에 $m$이 증가하고 $F[3]=2$가 된다.
- $begin=2$
- $m=2$
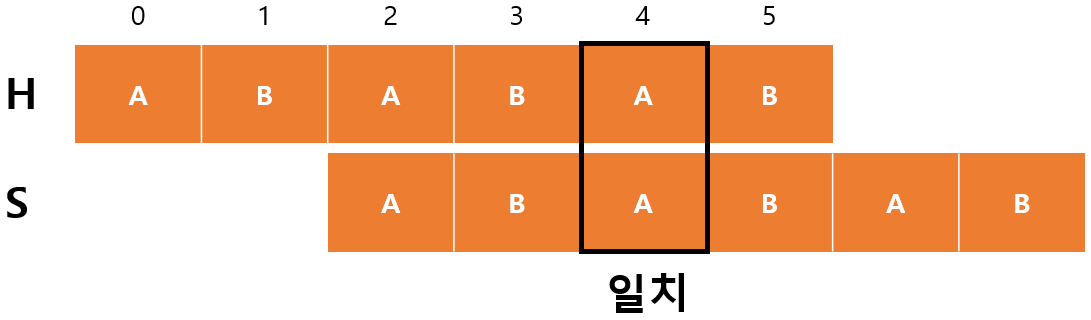
$H[4]$와 $S[2]$가 일치하기 때문에 $m$이 증가하고 $F[4]=3$이 된다.
- $begin=2$
- $m=3$
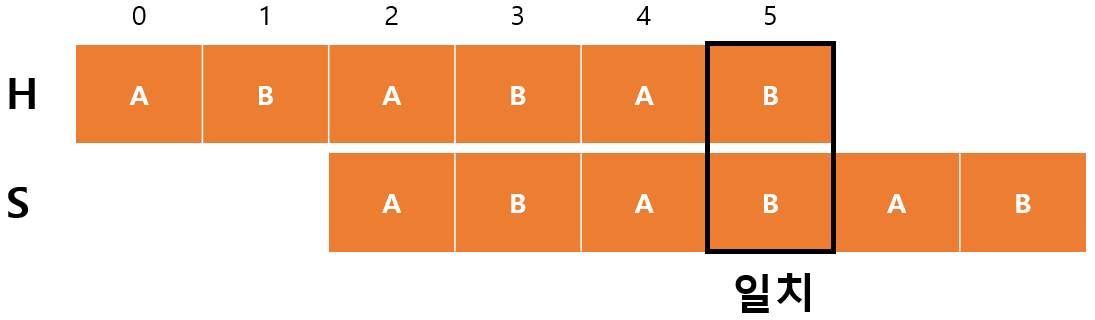
마지막으로 $H[5]$와 $S[3]$이 일치해서 $m$이 증가하고 $F[5]=4$가 된 후에 종료된다.
- $begin=2$
- $m=4$
여기서 주목할 점은 $m$이 증가하게 될 때 $begin$은 따로 증가하지 않는다는 점인데, 그 이유는 $H$의 인덱스가 $begin+m$으로 참조되기 때문이다. 불일치로 인해 실패 함수값을 쓰는 경우가 나오진 않았지만 원래의 KMP처럼 동작하기 때문에 똑같다고 할 수 있다.
이제 코드를 한번 확인해보자.
vector<int> failure_function(const string& S)
{
int n = S.length();
vector<int> f(n,0);
int begin = 1, m = 0;
// 끝까지 확인한다.
while(begin+m < n) {
// 일치하면 m을 증가시키고 실패함수를 초기화한다.
if(S[begin+m]==S[m]) {
m++;
f[begin+m-1] = m;
}
else {
if(m==0)
begin++;
else {
begin += (m - f[m-1]);
m = f[m-1];
}
}
}
return f;
}
사소한 부분을 제외하고는 거의 동일하게 동작한다는 것을 알 수 있다. 시간복잡도는 당연히 KMP를 활용하기 때문에 $S$의 길이를 $S_L$이라고 했을 때 $O(S_L)$만큼 나오게 된다. 결론적으로 KMP알고리즘의 최종 시간복잡도는 $O(H_L+S_L)$로 보통 $H_L \ge S_L$인 점을 감안하면 $O(H_L)$이라고도 할 수 있다.
References
- 라이(kks227)님의 KMP 알고리즘
- 알고리즘 문제 해결 전략, 20.2 문자열 검색